The Art of the Deal: Negotiations with Game Theory
Negotiation is not a one-step process; most of the time buyers and sellers go back and forth trying to get the best deal possible, and each step will alter the outcomes for both parties. With game theory, specifically with an extensive-form game, we can dissect these interactions into smaller sections and understand how negotiation unfolds over several rounds.
An extensive-form game is a key concept in game theory that represents strategic interactions among players in a sequential manner. Unlike normal-form games, which summarize strategies in a matrix, extensive-form games use a tree structure to illustrate the order of moves, choices available at each decision point, and the information players have when making those choices. Each node in the tree represents a point where a player can make a decision, and the branches indicate the possible actions they can take. At the end of the game, players receive payoffs based on the combination of choices made throughout the game. This format allows for a detailed analysis of strategies, including how players might react to others' moves. A critical method for solving extensive-form games is backward induction, where players anticipate future actions and outcomes by reasoning backwards from the end of the game to determine optimal strategies at earlier stages. Extensive-form games can also incorporate elements of chance and imperfect information, making them versatile for modelling real-world scenarios like negotiations or competitive situations where timing and knowledge significantly impact outcomes.
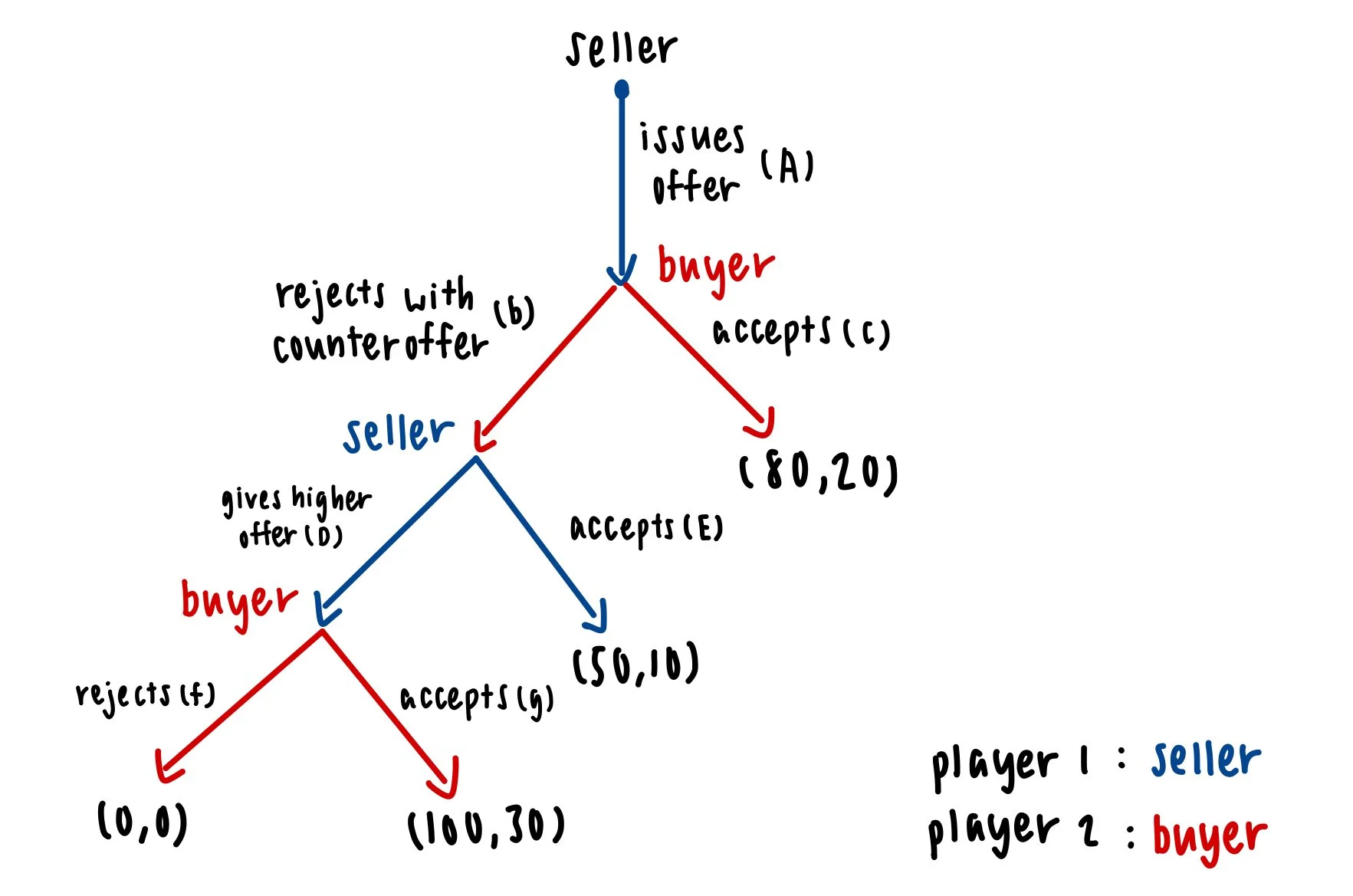
In the context of real estate negotiations, extensive form games provide a structured framework for analysing the interactions between key players—typically the buyer and the seller. Each participant comes to the table with distinct preferences, strategies, and potential outcomes that influence their decision-making processes. Assuming both parties are rational, sellers would most likely be aiming to make the most possible profit from the deal, while buyers would like to purchase the property at lower prices. To illustrate these dynamics, we construct a game tree for the scenario. Each node in this tree represents a critical decision point where players can choose among various actions: they may accept an offer, reject it and propose a counteroffer, or even decide to walk away from the negotiation entirely.
By mapping the decision-making process between the seller and buyer, you can see the sequential nature of negotiations. Compared to a normal-form matrix, the game tree can better reflect real-world negotiation dynamics, where each move influences future options and their corresponding payoffs. In sequential games, there is a specific type of equilibrium called a subgame perfect equilibrium (SPE). SPE refers to a strategy profile that represents optimal strategies for all players at every possible point in the negotiation process, ensuring that players make the best decisions given the actions of others.
Using the backward induction, the players will take the following actions for each subgame:
Subgame for actions f and g: the buyer (player 2) will take action g with payoff (100, 30) to maximize the buyer's payoff, so the payoff for action D becomes (100, 30).
Subgame for actions D and E: the seller (player 1) will take action D for 100 > 50, so the payoff for action b becomes (100, 30).
Subgame for actions b and c: the buyer (player 2) will take action b to maximize the buyer’s payoff, so the payoff for action A becomes (100, 30).
Thus, the subgame perfect equilibrium is {bg, AD} with the payoff (100, 30).
Nothing is perfect, and the same goes for market information. When one party in a transaction possesses more or superior information than the other, imperfect information occurs, leading to an imbalance that can affect decision-making. In real estate transactions, this is particularly prevalent, as sellers often have more knowledge about property values, market conditions, and potential issues than buyers. For example, a seller may be aware of structural problems or neighbourhood developments that could impact the property's value. At the same time, the buyer may only have access to public listings and general market trends. This disparity can significantly influence offers and counteroffers; a buyer might offer a lower price based on incomplete information, while the seller, knowing the true value, may counter with a higher price. Similarly, if a buyer has insider knowledge about an area’s future development plans, they might aggressively offer to secure the property before prices rise.
Like most models, using extensive form games to predict outcomes can only be done accurately under a list of pre-assumed conditions, which limits its practicality. Backward induction assumes players have complete knowledge of the game's rules, other players' strategies, and payoffs. In reality, perfect information does not exist and makes the game impractical. For example, poker players do not have complete information about their opponents' cards. While some players can deduce certain information based on experience, others may blindly make a move, which defies the assumption that all players are rational. Similarly, the logic assumes subgame perfection, meaning that players make optimal decisions at every node of the game tree. However, in reality, players may not always play optimally at every step, and emotions can influence a party's decisions, leading to outcomes different from those predicted.
As negotiations become increasingly complex, the need for sophisticated analytical tools becomes increasingly apparent. Extensive form games can provide a great starting point for understanding the sequential dance between buyers and sellers, but they are just one piece of the puzzle after all.